Electrical Grid Stability
Introduction
The goal of this project is to build a machine learning model that can predict the stability of an electrical grid based on various features such as the reaction time of each network participant, the nominal power produced or consumed by each participant, and the price elasticity coefficient for each participant. The dataset consists of 12 predictive features and two dependent variables: 'stab' and 'stabf'. The predictive features include:
tau1' to 'tau4': the reaction time of each network participant, a real value within the range 0.5 to 10 ('tau1' corresponds to the supplier node, 'tau2' to 'tau4' to the consumer nodes).
'p1' to 'p4': nominal power produced (positive) or consumed (negative) by each network participant, a real value within the range -2.0 to -0.5 for consumers ('p2' to 'p4'). As the total power consumed equals the total power generated, p1 (supplier node) = - (p2 + p3 + p4)
'g1' to 'g4' : price elasticity coefficient for each network participant, a real value within the range 0.05 to 1.00 ('g1' corresponds to the supplier node, 'g2' to 'g4' to the consumer nodes; 'g' stands for 'gamma')
The dependent variables are 'stab' (the maximum real part of the characteristic differential equation root) and 'stabf' (a categorical label indicating whether the system is stable or unstable)
UCI dataset link: https://archive.ics.uci.edu/ml/datasets/Electrical+Grid+Stability+Simulated+Data+#
Data Preprocessing
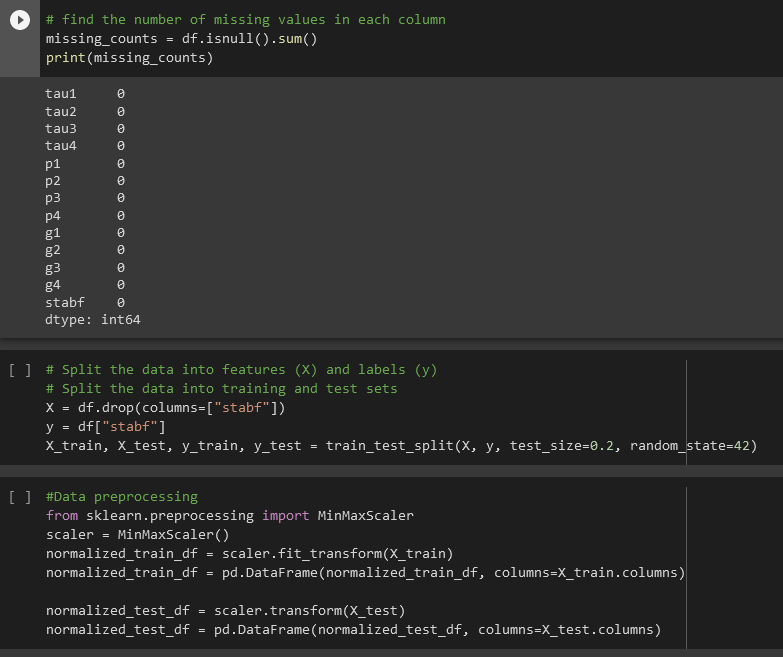
The data was preprocessed to handle missing values, scale the features, and split the data into training and testing set
Model training and evaluation
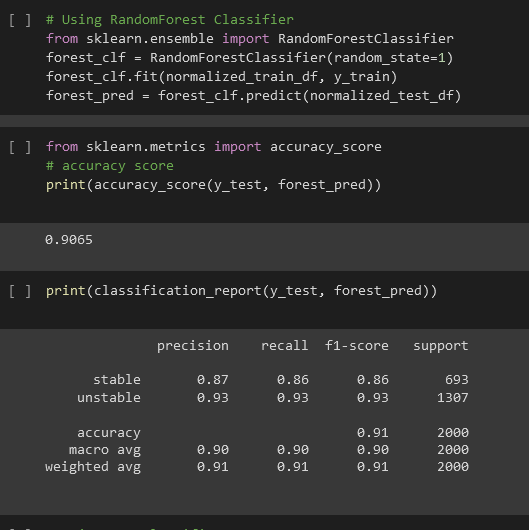
LightGBM and RandomForest Classifer was used to predict the stability of the electrical grid based on the predictive features. The model was trained using 80% of the data and evaluated on the remaining 20%. . The LightGBM Classifer achieved an accuracy of 94% and it was chosen based on the evaluation results
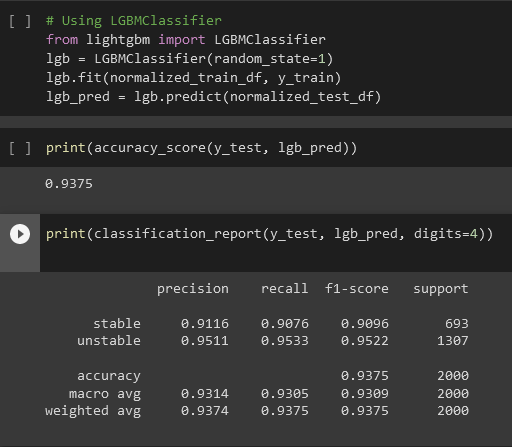
Conclusion
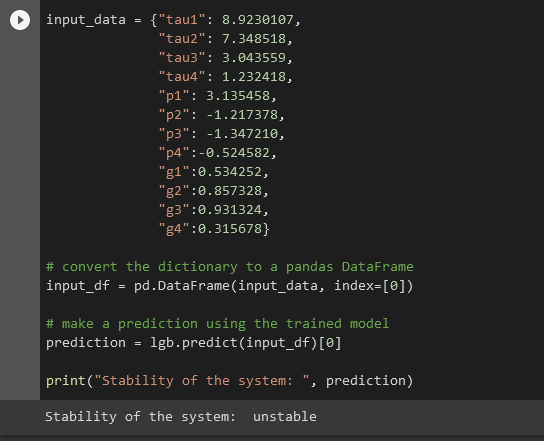
Overall, the model performed well, achieving high accuracy, precision and recall on the testing set. These results suggest that the model is able to effectively predict the stability of the electrical grid based on the predictive features. In future work, it would be interesting to explore other machine learning algorithms and techniques to further improve the model's performance. This model can be used to predict the stability of an electrical grid based on the input variables as shown below.